今天学习了周志华教授的西瓜书的第三章 - 线性模型,在知乎上看到了一些关于线性模型不错的理解,在此记录和分享一下
关于Logistic Regression处理非线性平面的问题
在看到 Andrew Ng 教授的机器学习中关于 Logistic Regression 的视频的时候,看到有关决策边界的内容,看到这个图的时候想着这只是线性的情况,那 Logistic Regression 是否能处理非线性的情况呢?
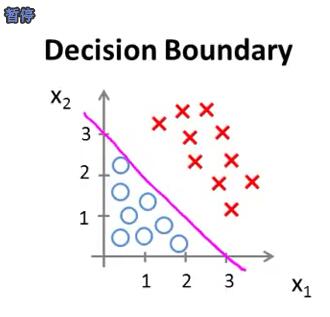
(原谅当时没看到视频的后面,其实视频的后面有提到非线性的情况)
Logistic Regression 其实是以线性回归算法为基础的,只不过Logistic Regression 模型中在计算最终结果时,为了将连续的结果转换为 [0. 1] 的概率值而引入了 sigmoid 函数映射.
这里重点说一下关于 “线性” 的理解
这里的“线性”指的是参数 θ 关于模型是线性关系,即以下关系:
但是,变量 $x_i$ 关于模型却可以是线性的或是非线性的,下面通过一个例子可以解释:
有一个二分类问题: 房子值不值得买(0 -> 值得买; 1 -> 不值得买)
此时假设有两个变量 $x_0$ & $x_1$ 分别代表房子的长度和房子的宽度,而特征有两个: $f1=x_1$ (房子的长度) ; $f_2=2x_2$(两倍的房子的宽度),此时可以用公式:
表示,此时无论是模型关于 参数 还是 模型 关于变量$x_0$、 $x_1$都是 线性的关系。如果房子值不值得买符合线性关系,那么这个时候就已经解决问题了,但是,如果问题并不是一个简单的线性模型,即分类平面不是线性的关系(重点来了,这里的不是线性的关系指代的是模型结果关于$x_0$和$x_1$不是线性关系)
这个时候我们可以利用 $x_0$ 和 $x_1$ 构造出一个非线性的关系出来,例如构造出一个新的变量 $x_1=x_1^2+12$ 这个时候模型关于新的变量就不是线性关系了。
但是注意:此时的模型关于参数 θ 任然是线性的,也即最后训练出来的模型任然是一个线性模型,只不过我们构造出了关于模型的非线性特征使得模型能够更好的拟合到数据中的非线性的特点。
这里再举一个栗子:
假如我们要实际预测的问题的分布是这样的:
此时,分布属于非线性的情况,因为我们有两个变量:$x_1$ 和 $x_2$,如果仅用 $x_1$ 和 $x_2$ 的线性组合我们永远也无法很好的拟合这些数据
但是,如果我们将原来的 $x_1$ 和 $x_2$ 映射为:$x_1^{‘}=x_1^2$ 和 $x_2^{‘}=x_2^2$ 这个时候模型关于新的变量 $x_1^{‘}$ 和 $x_2^{‘}$ 就是线性的关系了,我们可以用:
表示新的模型,从而很好的拟合原有的数据
从上面的例子我们可以看出,在对Logistic Regression建模的过程中,特征的构建显得很重要。当数据分布对应非线性时,我们就需要找到合适的映射函数 $\phi(x)$ 使得模型能够很好的处理非线性决策边界
总结一下
对于Logistic Regression 来说本质上属于线性回归模型,因为模型关于系数 θ 是线性函数
对于分离平面,无论是线性的还是非线性的,Logistic Regression 其实都可以分类,只不过对于非线性的情况下需要自己去寻找关于原变量的一个非线性映射(如例子中的 $x_1\to x_1^2$)
对于非线性情况下的映射函数的构建至关重要,决定了模型能否很好的拟合非线性决策边界
等看到 SVM 的时候会把Logistic Regression 和 SVM 针对线性情况和非线性情况再做一个对比
原知乎的答案如下:
题主提到了SVM,区别是,SVM如果不用核函数,也得像逻辑回归一样,在映射后的高维空间显示的定义非线性映射函数$\phi$,而引入了核函数之后,可以在低维空间做完点积计算后,映射到高维
原知乎连接:逻辑斯蒂回归能否解决非线性分类问题? - 辛俊波的回答 - 知乎
https://www.zhihu.com/question/29385169/answer/44177582

